

In simple terms, if there are n observations, one is free to select the (n-1) observations in any order. Degrees of freedom denotes the number of decisions or the number of variables that are independent. Presumably the intent in using $\nu$ is for the same reason we often use $\text$ as a visual approximation. Degrees of freedom is a concept used for various statistical tests. What is degree of freedom in statistics Ask Question Asked 10 years, 7 months ago Modified 1 year, 8 months ago Viewed 47k times 28 In statistics, degree of freedom is widely used in regression analysis, ANOVA and so on. The number of degrees of freedom selects a single probability distribution from among infinitely many. Depending on the sample size, different degrees of freedom will display.
If you're using a text, I'd suggest that unless there's a good reason to do otherwise, you just use what the text uses. Updated on JanuMany statistical inference problems require us to find the number of degrees of freedom. The degrees of freedom is df number of categories lk where l is the number of constraint, usually when the sum of expected counts adds up to the sum of observed counts, this is one. In statistics, degrees of freedom define the shape of the t-distribution used in t-tests when calculating the p-value. Mathematically, degrees of freedom is the number of dimension of the domain of a random vector, or essentially the number of 'free' components: how many components need to be known before the vector is fully determined.

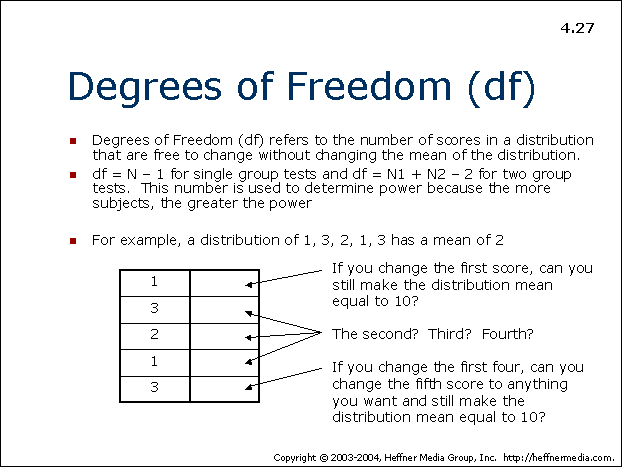
Where feasible, I think conventional notation is better, since it's likely to agree with more sources, and the Greek-letters-for-parameters is pretty well established. The number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary. Total sum of squares sum of squares due to regression + sum of squared errors, i.e. You can define your notation is almost any convenient way as long as it's clear, but $\nu$, the Greek letter is probably the most traditional/widely used for the $t$ and $\chi^2$ distributions at least. I'm trying to understand the concept of degrees of freedom in the specific case of the three quantities involved in a linear regression solution, i.e. I'll assert this without any attempt to offer evidence. It's calculated as the sample size minus the number of restrictions. Report the chi-square alongside its degrees of freedom, sample size, and p value, following this format: 2 (degrees of freedom, N sample size) chi-square value, p p value). The most common convention in statistics is to use Greek letters for parameters ($\mu, \sigma$ for normal distributions, $\lambda$ for Poisson, $\beta$ when parameterizing the mean in regression and GLMS, etc). Degrees of freedom, often represented by v or df, is the number of independent pieces of information used to calculate a statistic. Provide two significant digits after the decimal point.


 0 kommentar(er)
0 kommentar(er)
